10642. Можете ли Вы это решить?
Рассмотрим декартову систему
координат:
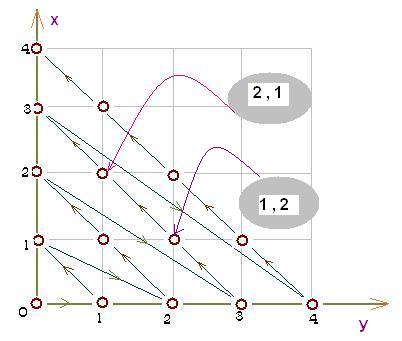
Совершается обход вершин
прямоугольной сетки, начиная с точки (0,
0) согласно направлению стрелок. Например, чтобы попасть с точки (0, 3) до (3,
0) следует пройти точки (1, 2) и (2, 1), сделав при этом 3 перемещения по
стрелкам. В задаче требуется найти количество перемещений, за которое можно
попасть из точки с координатами (x1, y1) в
точку с координатами (x2, y2), если известно,
что это всегда можно сделать.
Вход.
Первая строка содержит количество тестов n (0 < n £ 500). Каждая следующая строка содержит координаты точек (x1,
y1) и (x2, y2).
Выход. Для каждого теста вывести число
перемещений, которое следует совершить для попадания из точки (x1,
y1) в (x2,
y2).
Пример входа
30 0 0 10 0 1 00 0 0 2
Пример выхода
Case 1: 1Case 2: 2Case 3: 3
РЕШЕНИЕ
сетки
Анализ алгоритма
Вычислим количество перемещений,
которое следует совершить для попадания по стрелкам из точки (0, 0) в точку (x,
y). Движение происходит по диагоналям. Для попадания на первую диагональ,
соединяющую точки (0, 1) и (1, 0), достаточно совершить одно перемещение из (0,
0) в (0, 1). Для попадания во вторую диагональ, соединяющую точки (0, 2) и (2,
0), из начала первой диагонали (точки (0, 1)), необходимо совершить два
перемещения. И так далее: для попадания в k - ую диагональ, соединяющую
точки (0, k) и (k, 0), из начала (k – 1) - ой диагонали (точки (0, k – 1)), необходимо совершить k перемещений.
Точка (x, y)
находится на диагонали номер x + y. Для достижения этой диагонали
следует совершить 1 + 2 + ... + (x + y – 1) + (x + y) = (1 + x + y) * (x + y)
/ 2 = (x + y) * (x + y + 1) / 2 шагов. Попав за это
количество шагов в точку (0, x + y), еще следует пройти x
шагов чтобы попасть в точку (x, y). Таким образом, число
перемещений из (0, 0) в (x, y) равно dist(x, y) = (x
+ y) * (x + y + 1) / 2 + x.
Чтобы попасть из точки (x1,
y1) в точку (x2, y2) следует
совершить dist(x2, y2) – dist(x1,
y1) перемещений.
Пример
Рассмотрим третий тест. Чтобы
попасть из точки (0, 0) в точку (0, 2) следует пройти точки (0, 1), (1, 0),
сделав при этом 3 перемещения:
dist(0, 2) = (0 + 2) * (0 + 2 + 1) / 2 + 0
= 3
Реализация алгоритма
Функция вычисления числа
перемещений от точки (0, 0) до (x, y) имеет вид:
int dist(int x, int y)
{
return (1+x+y) * (x+y) / 2 + x;
}
Обрабатываем последовательно
тесты. Для каждой входной пары точек (x1, y1)
и (x2, y2) вычисляем и выводим значение
dist(x2, y2) – dist(x1, y1).
scanf("%d",&n);
for(i = 0; i < n; i++)
{
scanf("%d %d %d %d",&x1,&y1,&x2,&y2);
res = dist(x2,y2) - dist(x1,y1);
printf("Case %d: %d\n",i+1,res);
}